Answer:
perpendicular
Explanation:
Calculate the slopes m of the lines using the slope formula
m =
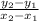
with (x₁, y₁ ) = J (11, - 2 ) and (x₂, y₂ ) = K (3, - 2 )
 =
=
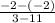 =
=
 =
=
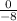 = 0
= 0
A line with a slope of 0 is a horizontal line parallel to the x- axis
Repeat with (x₁, y₁ ) = L (1, - 7 ) and (x₂, y₂ ) = M (1, - 2 )
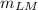 =
=
 =
=
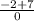 =
=
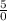 ← undefined slope
← undefined slope
A line with an undefined slope is a vertical line parallel to the y- axis
Since JK is horizontal and LM is vertical then they are perpendicular.