Question

A) Consider an air standard otto cycle that has a heat addition of 2800 kJ/kg of air, a compression ratio of 8 and a pressure and temperature at the beginning of compression process of 1 bar, 300 k. Determine:

(i) Maximum pressure and temperature in the cycle
(ii) Thermal efficiency
(iii) Mean effective pressure.
Assume for air Cp = 1.005 kJ/kg K, Cp = 0.718 kJ/kg K and R = 287 kJ/kg K.
(b) Explain any four types of classification of an Internal combustion engines.
:

Answer 1

a) i) The maximum pressure is approximately 122.37 bar

ii) The thermal efficiency is approximately 56.47%

iii) The mean effective pressure is approximately 20.974 bar

b) (b) Four types of internal combustion engine includes;

1) The diesel engine

2) The Otto engine

3) The Brayton engine

4) The Wankel engine

Step-by-step explanation:

The parameters of the Otto cycle are;

The heat added,
`Q_(in)` = 2,800 kJ/kg

The compression ratio, r = 8

The beginning compression pressure, P₁ = 1 bar

The beginning compression temperature, T₁ = 300 K

Cp = 1.005 kJ/kg·K

Cv = 0.718 kJ/kg·K

R = 287 kJ/kg·K

K = Cp/Cv = 1.005 kJ/kg·K/(0.718 kJ/kg·K) ≈ 1.4

T₂ = T₁×r^(k - 1)

∴ T₂ = 300 K×8^(1.4 - 1) ≈ 689.219 K

`(P_1\cdot V_1)/(T_1) = (P_2\cdot V_2)/(T_2)`

`P_2 = (P_1\cdot V_1 \cdot T_2)/(T_1 \cdot V_2) = (V_1)/(V_2) \cdot (P_1 \cdot T_2)/(T_1 ) = r \cdot (P_1 \cdot T_2)/(T_1 )`

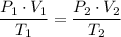
∴ P₂ = 8 × 1 bar × (689.219K)/300 K ≈ 18.379 bar

`Q_(in)` = m·Cv·(T₃ - T₂)

∴
`Q_(in)` = 2,800 ≈ 0.718 × (T₃ - 689.219)

T₃ = 2,800/0.718 + 689.219 = 4588.94 K

P₃ = P₂ × (T₃/T₂)

P₃ = 18.379 bar × 4588.94K/(689.219 K) = 122.37 bar

The maximum pressure = P₃ ≈ 122.37 bar

(ii) The thermal efficiency,
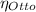`\eta_(Otto)`, is given as follows;

`\eta_(Otto) = 1 - (1)/(r^(k - 1))`

Therefore, we have;

`\eta_(Otto) = 1 - (1)/(8^(1.4 - 1)) \approx 0.5647`

The thermal efficiency,
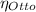`\eta_(Otto)` ≈ 0.5647

Therefore, the thermal efficiency ≈ 56.47%

(iii) The mean effective pressure, MEP is given as follows;

`MEP = (\left(P_3 - P_1 \cdot r^k \right) \cdot \left(1 - (1)/(r^(k-1)) \right))/((k -1)\cdot (r - 1))`

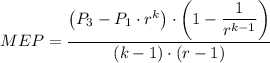
Therefore, we get;

`MEP = (\left(122.37 - 1 * 8^(1.4) \right) \cdot \left(1 - (1)/(8^(1.4-1)) \right))/((1.4 -1)\cdot (8 - 1)) \approx 20.974`

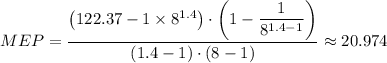
The mean effective pressure, MEP ≈ 20.974 bar

(b) Four types of internal combustion engine includes;

1) The diesel engine; Compression heating is the source of the ignition, with constant pressure combustion

2) The Otto engine which is the internal combustion engine found in cars that make use of gasoline as the source of fuel

The Otto engine cycle comprises of five steps; intake, compression, ignition, expansion and exhaust

3) The Brayton engine works on the principle of the steam turbine

4) The Wankel it follows the pattern of the Otto cycle but it does not have piston strokes