The question is incomplete. Here is the complete question.
An employee's salary, S(n), in dollars, at a company is a function of the number of years, n, that the employee has worked at the company.
The relationship between n and S(n) is shown in the table below.
Which of the following equations represents an explicit formula for S(n)?
A. S(n) = 40,000(1.05)ⁿ
B. S(n) = 40,000 + 1.05n
C. S(n) = 40,000(1.05)ⁿ⁻¹
D. S(n) = 40,000 + 1.05(n-1)
Answer: A. S(n) = 40,000(1.05)ⁿ
Explanation: The table shows an exponential function, which is, in general, is of the form:
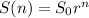
where
S₀ is the initial value
r is the rate the salary grows
n is the years the employee worked
From the table, in the first year, an employee receives $40,000, so, that is the initial value.
The salary increases at a constant rate of 1.05 per year, as shown below:
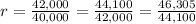
r = 1.05
So, the rate the salary grows is r = 1.05 or 5%.
Therefore, the equation that shows an explicit formula for S(n) is
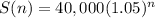 .
.