Given:
Width of the rectangular yard = x feet
Length of the rectangular yard = x+4 feet
Perimeter of the rectangular yard is:
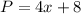
Perimeter of the yard = 84 feet
To find:
The length of the rectangular yard.
Solution:
Perimeter of the yard is 84 feet.
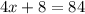
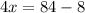
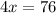
Divide both sides by 4.
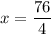
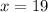
So, the width of the rectangular yard is 19 feet.
Length =
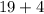
Length =
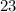
The length of the rectangular field is 23 feet.
Therefore, the correct option is B.