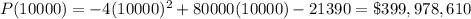Answer:
10,000 pPhones.
Explanation:
The cost to manufacture x pPhones is given by the cost function:
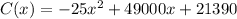
And the revenue for selling x pPhones is given by the revenue function:
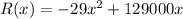
We want to determine the number of pPhones the Pear Company should sell to maximize profits.
First, we can find the profit function. Profit is given by:

Therefore:
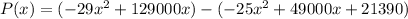
Simplify:

Add. So, our profit function is:
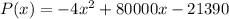
Note that our profit function is a quadratic. The maximum point of a quadratic is always its vertex. So, we can find the vertex of the profit function.
The coordinate of the vertex is given by:
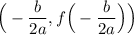
In this case, a = -4, b = 80000, and c = - 21390.
Therefore, the point at which profit is maximized is:
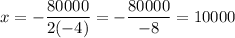
Therefore, in order to maximize profits, the Pear Company should sell exactly 10,000 phones.
Notes:
And the maximum profit will be: