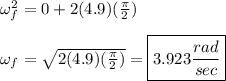Hi there!
Assuming the rod is pulled back 90° (π/2 radians), we can use angular kinematics to solve.
Using the equation:

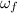 = final angular velocity (? rad/sec)
= final angular velocity (? rad/sec)
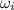 = initial angular velocity (0 rad/sec)
= initial angular velocity (0 rad/sec)
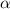 = angular acceleration (rad/sec², must solve for)
= angular acceleration (rad/sec², must solve for)
 = angular displacement (π/2 rad)
= angular displacement (π/2 rad)
Recall Newton Second Law's rotational equivalent:

τ = Torque (Nm)
I = Moment of inertia (kgm²)
α = angular acceleration (rad/sec²)
Setting the pivot point at the end, and knowing that the force of gravity works at an object's center of mass (1.5m from the rod's end), we can solve for the angular acceleration.
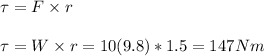
Now, solve for the moment of inertia given I = 1/3ML² at one of its ends:
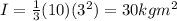
Solve for the angular acceleration:
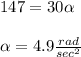
Now, we can use the kinematic equation to solve.