Answer:
1) D.
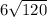 , 2) C.
, 2) C.
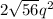 , 3) C.
, 3) C.
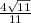
Explanation:
1) We proceed to simplify the expression given in statement:
(i)
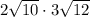 Given
Given
(ii)
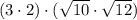 Commutative and associative properties
Commutative and associative properties
(iii)
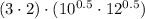 Definition of square root.
Definition of square root.
(iv)
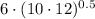 Definition of multiplication/
Definition of multiplication/
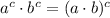
(v)
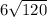 Definition of multiplication/Definition of square root/Result
Definition of multiplication/Definition of square root/Result
Answer: D
2) We proceed to simplify the expression given in statement:
(i)
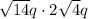 Given
Given
(ii)
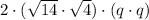 Commutative and associative properties
Commutative and associative properties
(iii)
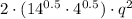 Definition of square root/Definition of power.
Definition of square root/Definition of power.
(iv)
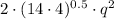
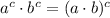
(v)
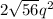 Definition of multiplication/Definition of square root/Result
Definition of multiplication/Definition of square root/Result
Answer: C
3) We proceed to simplify the expression given in statement:
(i)
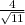 Given
Given
(ii)
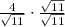 Modulative property/Existence of multiplicative inverse.
Modulative property/Existence of multiplicative inverse.
(iii)
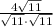
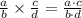
(iv)
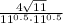 Definition of square root.
Definition of square root.
(v)
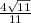
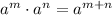 /Result
/Result
Answer: C