Question

The surveillance camera on a satellite at 250 km above the earth is taking pictures of the earth surface. Suppose that the imaging wavelength is 550 nm and the diameter of the camera lens is 40 mm. (a) Calculate the angular resolution of the camera. (b) Suppose that the headlights of a car on the earth are 1.6 m apart, can the camera resolve them

Answer 1

a) θ = 1.67 10⁻⁵ m, b) Consequently we must affirm that the vehicle headlights cannot resolve.

Step-by-step explanation:

a) To find the resolution of the camera we use the Rayleigh criterion for diffraction

a sin θ = m λ

where m = 1 for the first zero of the slit

we must remember that the angles in the experiments are measured in radians and are very small

sin θ = θ

we substitute

θ =
`(\lambda)/(a)`

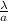
this expression is for a slit, in the case of circular openings the expression must be solved in polar coordinates giving

θ =
`1.22 \ (\lambda)/(D)`

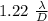
where D diameters of the opening

let's calculate

θ =
`1.22 \ (550 \ 10^(-9))/( 40\ 10^(-3))`

θ = 1.67 10⁻⁵ m

b) let's use trigonometry to find the separation distance on earth

tan θ = y / x

y = x tan θ

let's calculate

remember that the angles must be in radians

y = 250 10³ tan 1.67 10⁻0-5

y = 4.18 m

as they indicate that the separation of the headlights is y = 1.6m,

we see that this separation is greater than the separation distance separation.

Consequently we must affirm that the vehicle headlights cannot resolve.