Answer:
Points of intersection of these graphs are (-2, -3) and (0.6, 4.8).
Explanation:
Equation of the circle → (x - 2)² + y² = 25 ---------(1)
→ (x - 2)² + (y - 0)² = 5²
By comparing this equation with the standard equation of the circle,
(x - a)² + (y - b)²= r²
Here (a, b) is the center and r is the radius of the circle.
Therefore, center of the circle is (2, 0) and radius = 5 units
Second equation is a linear equation → y = 3x + 3 -------(2)
x-intercept of the equation → x = -1
y-intercept of the equation → y = 3
By graphing these equations we can get the point of intersections.
Solving these equations algebraically,
Substitute the value of y from equation (2) in the equation (1),
(x - 2)² + (3x + 3)² = 25
x² - 4x + 4 + 9x² + 18x + 9 = 25
10x² + 14x - 12 = 0
5x² + 7x - 6 = 0
x =
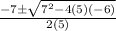
x =
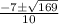
x =
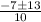
x = -2, 0.6
From equation (2),
y = -3, 4.8
Therefore, points of intersection of these graphs are (-2, -3) and (0.6, 4.8).