Answer:
The algorithm is as follows:
1. Start
2. Get the number of items (n)
3. Get the current price of the n items (a1, a2..... an)
4. Get the possible hiked price of the n items (b1, b2..... bn)
5. Calculate the difference between the current and hiked prices for each item i.e.
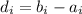
6. Sort the differences in descending order (i.e. from the greatest to the least)
7. Buy items in this order of difference
8. Stop
Explanation:
The algorithm is self-explanatory; however, what it does is that:
It takes a list of the current price of items (say list a)
E.g:
![a = [100, 150, 160]](https://img.qammunity.org/2022/formulas/computers-and-technology/college/cz6orst8ywrxvc3lk6ldz2exps1yflq7vr.png)
Then take a list of the hiked price of the items (say list b)
E.g:
![b = [110, 180, 165]](https://img.qammunity.org/2022/formulas/computers-and-technology/college/xo6vllwumtwn0gnl4j4r3r4eljkw0cqfln.png)
Next, it calculates the difference (d) between corresponding prices
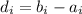
![d = [(110 - 100),(180-150),(165-160)]](https://img.qammunity.org/2022/formulas/computers-and-technology/college/kuh1neoq6letesqeuft7x8uobipd4o7skb.png)
![d = [10,30,5]](https://img.qammunity.org/2022/formulas/computers-and-technology/college/x0o5asx0qkqjcf64bzqdxsynar9z5bneut.png)
Sort the difference from greatest to lowest (as the difference is sorted, lists a and b are also sorted)
![d = [30,10,5]](https://img.qammunity.org/2022/formulas/computers-and-technology/college/r3mjheneb6mcuwrfhann5c50tkuwla75oy.png)
![a = [150, 100, 160]](https://img.qammunity.org/2022/formulas/computers-and-technology/college/kuzatzv2b6w6t8hsvc1wai2mvj6zplp7mf.png)
![b = [180, 110, 165]](https://img.qammunity.org/2022/formulas/computers-and-technology/college/3m8hgj0901x5q87s9q5s79tky96yzjtzv9.png)
If there is no hike up to item k, the couple would have saved (i = 1 to d[k-1])
Assume k = 3
The couple would have saved for 2 item
![Savings = d[1] + d[2]](https://img.qammunity.org/2022/formulas/computers-and-technology/college/3s95afucg5xdluwod2vmdrolzxcet1wa5f.png)
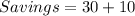
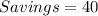
The saved amount will then be added to the kth item in list a i.e. a[k](in this case k = 3) in order to buy b[k]
Using the assumed value of k
![a[k] = a[3]](https://img.qammunity.org/2022/formulas/computers-and-technology/college/7k4jlldewnnml3fnstwo57hpwl0tqc34qz.png)
![a[3] = 160](https://img.qammunity.org/2022/formulas/computers-and-technology/college/yfiiv43x9yzcmsg1lvnthuk9ojspqlatac.png)
![b[3] = 165](https://img.qammunity.org/2022/formulas/computers-and-technology/college/e6oxu4pkofyphehrrg4h23aqiuf8hka46g.png)
Add the saved amount (40) to a[3]
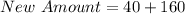
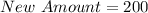
This new amount can then be used to buy b[3] i.e. 165, then they save the change for subsequent items