Which of the graphs below would result if you made the leading term of the following function negative? F(x) = x^3 + 3x^2

Question

asked Jan 21, 2023 31.1k views

2 Answers

Rodrigo Werlang · Answer 1 · 2023-01-25T22:37:50+0000

Answer:

D

Explanation:

Cubic equation: an algebraic equation of degree three and of the form

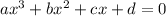ax^3 + bx^2 + cx + d = 0 , where a, b and c are the coefficients and d is the constant.

If the leading coefficient
of a cubic equation is positive, the curve begins in quadrant III and ends in quadrant I

If the leading coefficient
of a cubic equation is negative, the curve begins in quadrant II and ends in quadrant IV

For information

Graph A = cubic function with positive leading coefficient

Graph B = quadratic function with positive leading coefficient

Graph C = quadratic function with negative leading coefficient

Graph D = cubic function with negative leading coefficient

Therefore, if you made the leading coefficient of
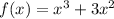f(x)=x^3+3x^2 negative, it would be graph D.