Answer:
The rate of conductive heat transfer Q/t is approximately 3.158 Watts
Step-by-step explanation:
The given parameters of the Styrofoam cup are;
The thermal conductivity of the cup, k = 0.010 W/(m·°C)
The cross-sectional area of the cup, A = 3.0 × 10⁻² m²
The thickness of the cup, L = 0.589 cm = 0.00589 m
The temperature of the coffee (in the cup) = 89°C, T₂ = 86.0 °C
The temperature of the air in the room (of the cup of coffee), T₁ = 24.0°C
The rate of conductive heat transfer of the cup of coffee, Q/t, is given by the following formula;
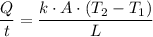
Plugging in the value of the variables, in the above equation, gives;
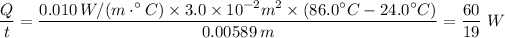
The rate of conductive heat transfer of the cup of coffee, Q/t = 60/19 W =
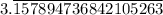 W ≈ 3.158 W.
W ≈ 3.158 W.