Question

(a) Show that the volume of a metal sphere of radius 15 cm is 14140 cm”, correct to 4 significant

figures
[The volume, V. of a sphere with radius r' is V=
V=tr'
(b) (i)
The sphere is placed inside an empty cylindrical tank of radius 25 cm and height 60 cm.
The tank is filled with water.
25 cm
NOT TO
SCALE
60 cm
Calculate the volume of water needed to fill the tank​

Answer 1

a) The volume of the sphere is approximately 14,137.16694 which is 14,140 cm³ correct to 4 significant figures

b) The volume of water required to fill the tank is approximately 103,670 cm³

Explanation:

a) In the question, the radius of the sphere, r = 15 cm

The formula for the volume, 'V', of a sphere is given as follows;

`V = (4)/(3) * \pi * r^3`

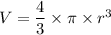
Where;

r = The radius of the the sphere

V = The volume of the sphere

Plugging in the value for the radius, 'r', of the sphere, in the equation for, 'V', we get;

`V = (4)/(3) * \pi * 15^3 \approx = 14,137.16694`

Therefore;

The volume of the sphere to 4 significant figures is V ≈ 14,140 cm³

b) The parameters of the cylindrical tank are;

The height of the cylindrical tank, h = 60 cm

The radius of the cylindrical tank, r = 25 cm

The volume of a cylinder, V = π·r²·h

∴ The volume of the cylindrical tank without water, '
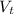`V_t`', is given as follows;

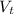`V_t` = π × (25 cm)² × 60 cm ≈ 117809.72451 cm³

The volume of water,
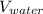`V_(water)`, required to fill the tank with the sphere of volume 'V' placed inside is given as follows

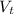`V_t` = V +
`V_(water)`

∴
`V_(water)` =
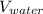
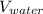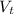`V_t` - V

From which we get;

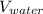`V_(water)` ≈ 117809.72451 cm³ - 14,140 cm³ = 103,669.72451 cm³ ≈ 103,670 cm³

The volume of water required to fill the tank,
`V_(water)` ≈ 103,670 cm³.