Answer:
Explanation:
Use SOH CAH TOA to recall how the trig functions fit on a triangle
SOH: Sin(Ф)= Opp / Hyp
CAH: Cos(Ф)= Adj / Hyp
TOA: Tan(Ф) = Opp / Adj
then
Sin(Ф) = -
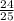
find the angle Ф
Ф = arcSin ( -
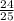 )
)
Ф = -73.739795°
so an angle measured clock wise from x axis at zero°
now use cos(Ф) = x/ 25 to find x
25* cos( -73.739795°) = x
7 = x :o wow... exactly? :P nice
cos(Ф) = 7/25 I think that's what they wanted to know
also I noted my calculator tried to find the fraction of 0.2800000049 and couldn't, but then I just put in 0.28 and it found that to be 7/25 :0 so I think we're spot on :)