Question

The angle 01 is located in Quadrant IV, and sin(01) = -24/ 25

What is the value of cos(01)?​

Answer 1

Explanation:

Use SOH CAH TOA to recall how the trig functions fit on a triangle

SOH: Sin(Ф)= Opp / Hyp

CAH: Cos(Ф)= Adj / Hyp

TOA: Tan(Ф) = Opp / Adj

then

Sin(Ф) = -
`(24)/(25)`

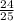
find the angle Ф

Ф = arcSin ( -
`(24)/(25)` )

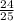Ф = -73.739795°

so an angle measured clock wise from x axis at zero°

now use cos(Ф) = x/ 25 to find x

25* cos( -73.739795°) = x

7 = x :o wow... exactly? :P nice

cos(Ф) = 7/25 I think that's what they wanted to know

also I noted my calculator tried to find the fraction of 0.2800000049 and couldn't, but then I just put in 0.28 and it found that to be 7/25 :0 so I think we're spot on :)

Answer 2

`(7)/(25)`

Explanation:

We can solve that using this identity,

`\sin {}^(2) (x) + \cos {}^(2) (x) = 1`

plug in -24/25 from x in sin

`\sin {}^(2) ( ( - 24)/(25) ) + \cos {}^(2) (x) = 1`

`\sin( (576)/(625) ) + \cos {}^(2) (x) = 1`

`\cos {}^(2) (x) = 1 - (576)/(625)`

`\cos {}^(2) (x) = (49)/(625)`

`\cos(x) = (7)/(25)`

Since cos is positve in quadrant 4, the answer is 7/25.