Answer:

Explanation:
We are given this function for the height (h) after t seconds:
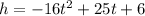
Seconds is t and we want to find the height after 1.5 seconds. Plug 1.5 in for t.
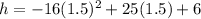
Solve according to PEMDAS: Parentheses, Exponents, Multiplication, Division, Addition, Subtraction.
Solve the exponent first.
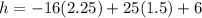
Multiply.
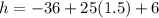
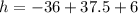
Add.
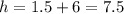
This is already rounded to the nearest tenth, so it is the answer.
After 1.5 seconds, the basketball is at a height of 7.5 feet.