Answer:
![\sqrt[7]{3^(2)}](https://img.qammunity.org/2022/formulas/mathematics/high-school/2v2rq36xsfge53020r2fj841lel7c84vro.png)
Explanation:
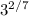
^ That is 3 to the 2/7ths power. We know that. Now it needs to be in radical form. That takes a bit of thinking.
If you have a power that is less than one (like 1/2) it is can be written as a root. So say you're given
 . That is the same exact thing as saying
. That is the same exact thing as saying
 . It's the same thing. You can say it either way.
. It's the same thing. You can say it either way.
In the same way, a squared power, like
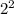 , is the same as representing it like a fraction, like
, is the same as representing it like a fraction, like
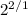 . They both mean the same thing.
. They both mean the same thing.
So by pointing these out, a fraction power = the power / the root.
If that makes sense.
So, with this in mind, let's look at what we have again.
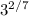
So we can split it up to say that 3 is raised to a 2nd power times a 1/7th power.
So we know what a 3 to the 2nd power is:
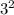 .
.
And since we have a fraction that's also included, we now know that is a root. So we can represent that like this:
![\sqrt[7]{3}](https://img.qammunity.org/2022/formulas/mathematics/high-school/q7jawd0wjr96i65v7pld6xrvbzlsyzej5c.png) .
.
But those two answers need to be combined. We can do that like this:
![\sqrt[7]{3^(2)}](https://img.qammunity.org/2022/formulas/mathematics/high-school/2v2rq36xsfge53020r2fj841lel7c84vro.png)
Answer:
![\sqrt[7]{3^(2)}](https://img.qammunity.org/2022/formulas/mathematics/high-school/2v2rq36xsfge53020r2fj841lel7c84vro.png)
So there it is! I hope that helped you!!