Question

Please help and explain this simple mathematics to me.

Thank you

Answer 1

I'll go over problem 9 part (a) to get you started.

The sine rule, aka law of sines, is this

`(\sin(A))/(a) = (\sin(B))/(b) = (\sin(C))/(c)`

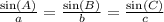
where the uppercase letters A,B,C are the angles and the lowercase letters a,b,c are the sides opposite those respective angles. Eg: angle B is opposite side b.

Some textbooks may have the lowercase letters up top, but it doesn't matter since it's the same ratio. All that matters is things stay consistent. The lowercase letters must be together on the same level, and same goes for the uppercase letters on their own separate level.

We can then break up that equation into these 3 separate equations, to make things more bite-sized so to speak.

`(\sin(A))/(a) = (\sin(B))/(b)\\\\(\sin(B))/(b) = (\sin(C))/(c)\\\\(\sin(A))/(a) = (\sin(C))/(c)\\\\`

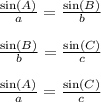
Let's focus on the 3rd equation and do a bit of algebraic manipulation like so

`(\sin(A))/(a) = (\sin(C))/(c)\\\\\sin(A) = (a\sin(C))/(c)\\\\(\sin(A))/(\sin(C)) = (a)/(c)\\\\`

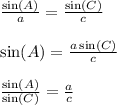
Through similar steps, we can say:

`(\sin(B))/(b) = (\sin(C))/(c)\\\\\sin(B) = (b\sin(C))/(c)\\\\(\sin(B))/(\sin(C)) = (b)/(c)\\\\`

-------------------------------------------

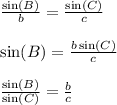
To summarize the previous section, we found that:

`(\sin(A))/(\sin(C)) = (a)/(c)\\\\(\sin(B))/(\sin(C)) = (b)/(c)\\\\`

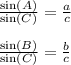
It then allows us to do the following steps for problem 9, part (a)

`(a+b)/(c) = (\sin(A)+\sin(B))/(\sin(C))\\\\(a+b)/(c) = (\sin(A))/(\sin(C))+(\sin(B))/(\sin(C))\\\\(a+b)/(c) = (a)/(c)+(b)/(c)\\\\(a+b)/(c) = (a+b)/(c)\\\\`

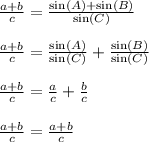
We have confirmed that the equation in problem 9 part (a) is indeed an identity. Take note how I kept the left hand side the same the entire time while the right hand side transformed into the left side.

Similar steps will be taken for problem 9, part (b). I'll let you do that part.