Answer:

Explanation:
Given function:
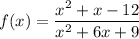
Factor the numerator:
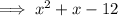
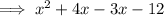
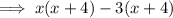

Factor the denominator:
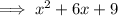
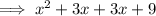
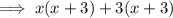

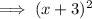
Therefore, the rational function is:
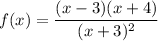
As the degree of the numerator is equal to the degree of the denominator, there is a horizontal asymptote at y = 1.
A vertical asymptote occurs at the x-value(s) that make the denominator of a rational function zero.

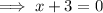
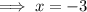
Therefore, there is a vertical asymptote at x = -3.
As there is a vertical asymptote at x = -3, the excluded x-value is x = -3.
As x approaches x = -3 from both sides, the numerator of the rational function approaches -6 and the denominator approaches a very small positive number. Therefore, the function approaches a very large negative number.
Therefore, the end behaviour of the function as it approaches the excluded value is: