Question

Determine whether the distribution represents a probability distribution. If not, identify any requirements that are not satisfied.

x P(x)
10.49
20.05
30.32
40.07
50.07

Answer 1

Answer: This is a valid probability distribution.

The P(x) values add to 1; each P(x) is between 0 and 1 inclusive.

============================================================

Further Explanation:

A valid probability distribution is when,

1. The P(x) values add to 1.
2. Each P(x) value is between 0 and 1 inclusive; i.e.
   `0 \le P(\text{x}) \le 1`

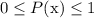
The given data table is:

`\begin{array} \cline{1-2}\text{x} & \text{P(x)}\\\cline{1-2}1 & 0.49\\\cline{1-2}2 & 0.05\\\cline{1-2}3 & 0.32\\\cline{1-2}4 & 0.07\\\cline{1-2}5 & 0.07\\\cline{1-2}\end{array}`

It's fairly clear that rule 2 has been satisfied. Something like
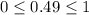`0 \le 0.49 \le 1` is indeed a true statement. It's like saying 49% is between 0% and 100%. The other P(x) values are similar in nature.

---------

Let's see what the P(x) probability values add to:

0.49+0.05+0.32+0.07+0.07 = 1

We see that rule 1 has been met as well.

Since both rules have been satisfied, this means we have a valid probability distribution.