Question

(PRE CALC)

What is the solution to the equation?

12ln(x+37)=ln(x2−25)−ln(x+5)

Responses

x = 1 and x = 12
x, = 1 and , x, = 12

x = 12 only
x, = 12 only

x=−12 only
x equals negative 12, only

x=−12 and x = 1

Answer 1

(a) x = 12 only

Explanation:

You want the solution to 1/2ln(x+37) = ln(x^2−25)−ln(x+5).

Graph

A graph of this written in the form ...

`(1)/(2)ln((x+37))-(ln((x^2-25))-ln((x+5)))=0`

shows one solution at x=12.

Antilog

The right side of the equation can be simplified to ...

`(1)/(2)\ln(x+37)=\ln{\left((x^2-25)/(x+5)\right)}=ln((x-5))\\\\x+37=(x-5)^2\qquad\text{multiply by 2; take antilogs}\\\\x^2-11x-12=0\qquad\text{subtract $x+37$}\\\\(x+1)(x-12)=0\qquad\text{factor}`

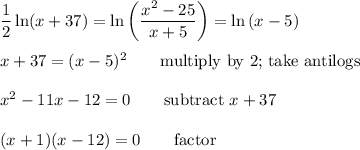
The argument of the ln function must be positive, so we require x > 5. The factors will be zero for x=-1 and x=12, but x=-1 is not in the domain of the original equation.

The only solution is x = 12.