Answer:
(a) x = 12 only
Explanation:
You want the solution to 1/2ln(x+37) = ln(x^2−25)−ln(x+5).
Graph
A graph of this written in the form ...
shows one solution at x=12.
Antilog
The right side of the equation can be simplified to ...
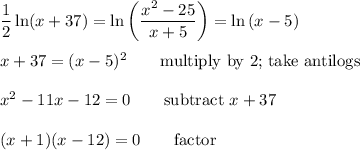
The argument of the ln function must be positive, so we require x > 5. The factors will be zero for x=-1 and x=12, but x=-1 is not in the domain of the original equation.
The only solution is x = 12.