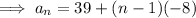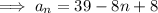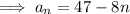Question

Write an explicit formula for an, the nth term of the sequence 39,31,23

Answer 1

`a_n=47-8n`

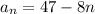
Explanation:

Given sequence:

• 39, 31, 23, ...

Calculate the differences between the terms:

`39 \underset{-8}{\longrightarrow} 31 \underset{-8}{\longrightarrow} 23`

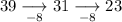
As the differences are constant (the same), this is an arithmetic sequence with:

• First term (a) = 39
• Common difference (d) = -8

`\boxed{\begin{minipage}{8 cm}\underline{General form of an arithmetic sequence}\\\\$a_n=a+(n-1)d$\\\\where:\\\phantom{ww}$\bullet$ $a$ is the first term.\\\phantom{ww}$\bullet$ $d$ is the common difference between terms.\\\end{minipage}}`

Substitute the found values of a and d into the formula to create an equation for the nth term of the sequence:

`\implies a_n=39+(n-1)(-8)`

`\implies a_n=39-8n+8`

`\implies a_n=47-8n`

Answer 2

a_n = 47 - 8n

Explanation:

a_1 = 39

a_2 = 31

a_3 = 23

31 - 39 = -8

23 - 31 = -8

This is an arithmetic sequence with constant difference -8.

a_1 = 39

a_2 = 39 - 8

a_3 = 39 - 8 - 8 = 39 - 2(8)

a_4 = 39 - 8 - 8 - 8 = 39 - 3(8)

...

a_n = 39 - (n - 1)(8)

a_n = 39 - 8(n - 1)

a_n = 39 - 8n + 8

a_n = 47 - 8n