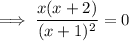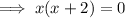Question

NO LINKS!!

Determine the open intervals on which the function is increasing, decreasing, or constant. (Enter the answers using interval notation. If an answer does not exist, enter DNE.)

f(x) = (x^2 + 2x + 2)/(x + 1)

increasing ______
decreasing _________
constant __________

Answer 1

Increasing: (-∞, -2) ∪ (0, ∞)

Decreasing: (-2, -1) ∪ (-1, 0)

Constant: x = 0, x = -2

Explanation:

A function is increasing when the gradient is positive ⇒ f'(x) > 0

A function is decreasing when the gradient is negative ⇒ f'(x) < 0

A function is constant when the gradient is zero ⇒ f'(x) = 0

Given function:

`f(x)=(x^2+2x+2)/(x+1)`

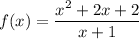
Differentiate the given function using the quotient rule.

`\boxed{\begin{minipage}{5.5 cm}\underline{Quotient Rule for Differentiation}\\\\If $y=(u)/(v)$ then:\\\\$\frac{\text{d}y}{\text{d}x}=\frac{v \frac{\text{d}u}{\text{d}x}-u\frac{\text{d}v}{\text{d}x}}{v^2}$\\\end{minipage}}`

`\textsf{Let}\;\;u=x^2+2x+2 \implies \frac{\text{d}u}{\text{d}x}=2x+2`

`\textsf{Let}\;\;v=x+1 \implies \frac{\text{d}v}{\text{d}x}=1`

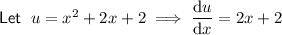
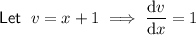
Therefore:

`\implies \frac{\text{d}y}{\text{d}x}=((x+1) (2x+2)-(x^2+2x+2))/((x+1)^2)`

`\implies \frac{\text{d}y}{\text{d}x}=(2x^2+4x+2-x^2-2x-2)/((x+1)^2)`

`\implies \frac{\text{d}y}{\text{d}x}=(x^2+2x)/((x+1)^2)`

`\implies \frac{\text{d}y}{\text{d}x}=(x(x+2))/((x+1)^2)`

`\implies f'(x)=(x(x+2))/((x+1)^2)`

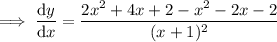
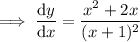
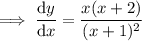
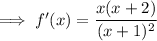
Find the critical values of the differentiated function (the zeros of the numerator and the denominator):

• Zeros of the numerator: x = 0, x = -2
• Zeros of the denominator: x = -1

Therefore, the intervals are:

• x < -2
• -2 < x < -1
• -1 < x < 0
• x > 0

Choose numbers that are within each interval and substitute them into the differentiated function:

`x < -2 \implies f'(-3)=(-3(-3+2))/((-3+1)^2)=(3)/(4) > 0`

`-2 < x < -1 \implies f'(-1.5)=(-1.5(-1.5+2))/((-1.5+1)^2)=-3 < 0`

`-1 < x < 0 \implies f'(-0.5)=(-0.5(-0.5+2))/((-0.5+1)^2)=-3 < 0`

`x > 0 \implies f'(1)=(1(1+2))/((1+1)^2)=(3)/(4) > 0`

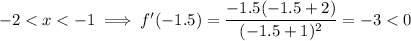
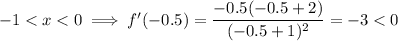
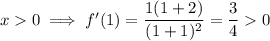
Increasing

Therefore, f'(x) > 0 when:

• x < -2 : (-∞, -2)
• x > 0 : (0, ∞)

Decreasing

Therefore, f'(x) < 0 when:

• -2 < x < -1 : (-2, -1)
• -1 < x < 0 : (-1, 0)

Constant

To find the interval where f(x) is constant, set the differentiated function to zero:

`\implies (x(x+2))/((x+1)^2) =0`

`\implies x(x+2) =0`

`\implies x=0 \;\; \textsf{or}\;\;x=-2`