Question

NO LINKS!!

The number of bacteria in a culture is increasing according to the law of exponential growth. The initial population is 240 bacteria, and the population after 7 hours is double the population after 1 hour. How many bacteria will be there after 4 hours? (Round your answers to the nearest whole number.)

Answer 1

381 bacteria

Explanation:

`\boxed{\begin{minipage}{9 cm}\underline{General form of an Exponential Function with base $e$}\\\\$y=Ae^(kt)$\\\\where:\\\phantom{ww}$\bullet$ $A$ is the initial value ($y$-intercept). \\ \phantom{ww}$\bullet$ $e$ is Euler's number. \\ \phantom{ww}$\bullet$ $k$ is some constant.\\ \phantom{ww}$\bullet$ $t$ is the independent value time.\\\end{minipage}}`

If the initial population is 240 bacteria, then A = 240:

`\implies y=240e^(kt)`

Create equations for the population after 1 hour and 7 hours:

`t=1\implies y=240e^(k)`

`t=7\implies y=240e^(7k)`

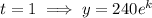
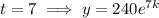
Given the population after 7 hours is double the population after 1 hour:

`\implies 240e^(7k)=2 \cdot 240e^k`

`\implies e^(7k)=2e^k`

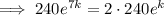
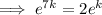
Solve the equation to find the value of k:

`\implies e^(7k)=2e^k`

`\implies (e^(7k))/(e^k)=2`

`\implies e^(6k)=2`

`\implies \ln e^(6k)=\ln 2`

`\implies 6k \ln e = \ln 2`

`\implies 6k=\ln 2`

`\implies k=(1)/(6)\ln 2`

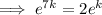
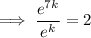
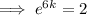
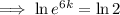
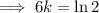
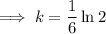
Therefore, the equation that models the given parameters is:

`y=240e^{(1)/(6)t\ln 2}`

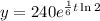
To find how many bacteria there will be after 4 hours, substitute t = 4 into the equation:

`\implies y=240e^{(1)/(6)(4)\ln 2}`

`\implies y=240e^{(2)/(3)\ln 2}`

`\implies y=240(1.58740105...)`

`\implies y=380.9762525`

`\implies y=381`

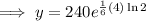
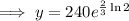
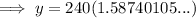
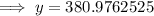
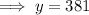
Therefore, there will be 381 bacteria after 4 hours