Answer:
381 bacteria
Explanation:

If the initial population is 240 bacteria, then A = 240:
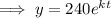
Create equations for the population after 1 hour and 7 hours:
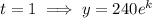
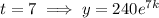
Given the population after 7 hours is double the population after 1 hour:
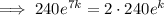
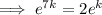
Solve the equation to find the value of k:
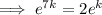
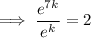
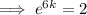
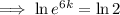
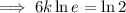
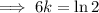
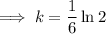
Therefore, the equation that models the given parameters is:
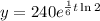
To find how many bacteria there will be after 4 hours, substitute t = 4 into the equation:
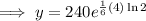
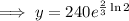
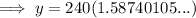
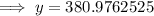
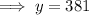
Therefore, there will be 381 bacteria after 4 hours