Answer:
Explanation:

Given:
- P = $18,000
- r = 1.5% = 0.015
Substitute the values of P and r into the formula for continuous compounding interest to create an equation for A in terms of t:
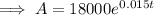
To complete the table, substitute each given value of t into the equation.
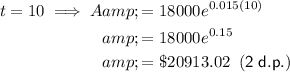
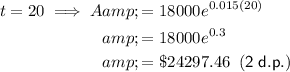
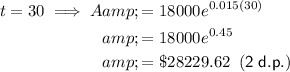
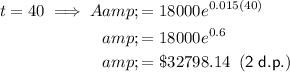
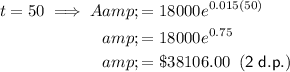
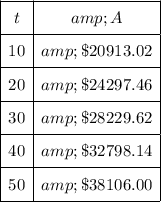
Completed table:
