Question

Show that 1/x is an integrating factor of the equation dy/dx-y/x = 3x​​

Answer 1

Suppose we're asked to solve the first order linear differnetial equation,

`\longrightarrow\rm{(dy)/(dx)+y\cdot P(x)=Q(x)}`

To solve this equation we have to find out a term called 'Integrating Factor' given by,

`\rm{I_f=e^(\int P(x)\ dx)}`

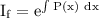
such that the solution of the equation is,

`\displaystyle\longrightarrow\rm{y\cdot I_f=\int Q(x)\cdot I_f\ dx}`

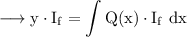
Here the given differential equation is,

`\longrightarrow\rm{(dy)/(dx)-(y)/(x)=3x}`

`\longrightarrow\rm{(dy)/(dx)+y\left(-(1)/(x)\right)=(3x)}`

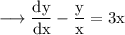
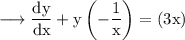
Here,

`\longrightarrow\rm{P(x)=-(1)/(x)}`

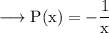
Integrating wrt x,

`\displaystyle\longrightarrow\rm{\int P(x)\ dx=-\int(1)/(x)\ dx}`

`\displaystyle\longrightarrow\rmx`

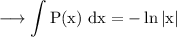
[We will consider constant of integration as zero.]

Then the integrating factor is,

`\longrightarrow\rm{I_f=e^(\int P(x)\ dx)}`

`\longrightarrow\rmx`

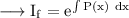
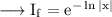
Since
`\rm{e^(b\,\ln(a))=a^b,}`

`\longrightarrow\rm{I_f=x^(-1)}`

`\longrightarrow\rm{\underline{\underline{I_f=(1)/(x)}}}`

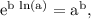
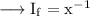
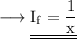
Hence the integrating factor for the given differential equation is 1/x.