Consider a cube of side a units, with sides along x, y and z axis and one vertex at origin, as in the figure.
Here AB and CD are two diagonals of the cube, because A and B are diagonally opposite corners, also C and D.
In the figure, coordinates of A is (0, 0, 0) and that of B is (a, a, a). Then vector AB is given by,

Coordinates of C is (a, 0, 0) and that of D is (0, a, a). Then vector CD is given by,
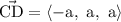
The diagonals each have a magnitude of a√3.

In the figure θ is the angle between the diagonals.
We take the dot product of the vectors AB and CD to get angle between them.
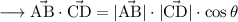
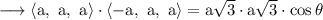
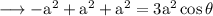

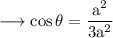
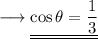
The angle between the diagonals satisfy this equation.
Hence Proved!