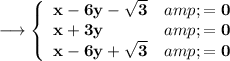Correct Question:-
Find the equations of lines normal to the curve
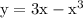 at points where it cuts the x axis.
at points where it cuts the x axis.

Solution:-
The given curve,
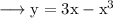
Differentiating wrt x we get,
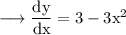
This term is slope of tangent on the curve at a point (x, y).
Taking reciprocal,
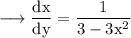
and multiplying by -1,
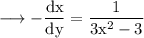
Now this term is slope of normal on the curve at a point (x, y).
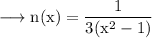

The points where the curve
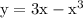 cuts x axis is obtained by equating y = 0.
cuts x axis is obtained by equating y = 0.
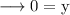
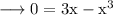
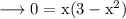
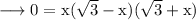
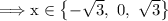
So the points where the curve cuts x axis are (-√3, 0), (0, 0) and (√3, 0).

Consider the point (-√3, 0).
The slope of normal at this point is,
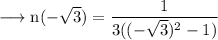
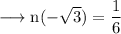
Then equation of normal at this point is,
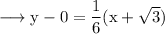
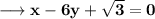

Consider the point (0, 0).
The slope of normal at this point is,
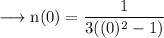
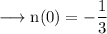
Then equation of normal at this point is,
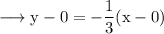
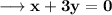

Consider the point (√3, 0).
The slope of normal at this point is,
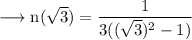
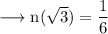
Then equation of normal at this point is,
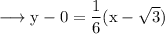
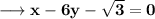

Hence the equations of lines normal to the curve
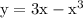 at points where it cuts x axis are,
at points where it cuts x axis are,