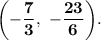Question

The points A ( 5, -2), B (2, 7), and C (-10, 4) are in the xy- plane. Find:

a. the equation of the line passing through A and parallel to BC,
b. the equation of the line passing through B, perpendicular to AC,
c. the point of intersection of the lines in (i) and (ii) above.​​

Answer 1

a. Finding equation of line passing through A and parallel to BC.

`\quad`

Since our line is parallel to BC, slope of the line is,

`\longrightarrow\rm{m_a=(y_B-y_C)/(x_B-x_C)}`

`\longrightarrow\rm{m_a=(7-4)/(2-(-10))}`

`\longrightarrow\rm{m_a=(1)/(4)}`

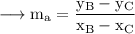
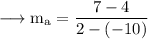
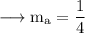
Since our line passes through A, the equation will be,

`\longrightarrow\rm{y-y_A=m_a(x-x_A)}`

`\longrightarrow\rm{y-(-2)=(1)/(4)(x-5)}`

`\longrightarrow\rm{\underline{\underline{x-4y-13=0}}\quad\quad\dots(1)}`

`\quad`

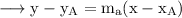
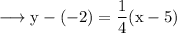
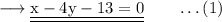
b. Finding equation of line passing through B and perpendicular to AC.

`\quad`

Since our line is perpendicular to AC, slope of the line is,

`\longrightarrow\rm{m_b=-(x_A-x_C)/(y_A-y_C)}`

`\longrightarrow\rm{m_b=-(5-(-10))/(-2-4)}`

`\longrightarrow\rm{m_b=(5)/(2)}`

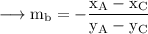
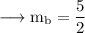
Since our line passes through B, the equation will be,

`\longrightarrow\rm{y-y_B=m_b(x-x_B)}`

`\longrightarrow\rm{y-7=(5)/(2)(x-2)}`

`\longrightarrow\rm{\underline{\underline{5x-2y+4=0}}\quad\quad\dots(2)}`

`\quad`

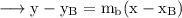
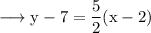
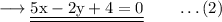
c. Finding point of intersection of the above two lines.

`\quad`

From (1),

`\longrightarrow\rm{x=4y+13}`

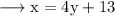
Putting this value of x in (2),

`\longrightarrow\rm{5(4y+13)-2y+4=0}`

`\longrightarrow\rm{18y+69=0}`

`\longrightarrow\rm{y=-(23)/(6)}`

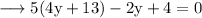
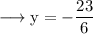
Then,

`\longrightarrow\rm{x=4\left(-(23)/(6)\right)+13}`

`\longrightarrow\rm{x=-(7)/(3)}`

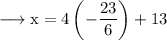
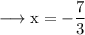
Hence the intersection point is
`\bf{\left(-(7)/(3),\ -(23)/(6)\right)}.`