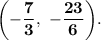a. Finding equation of line passing through A and parallel to BC.

Since our line is parallel to BC, slope of the line is,
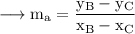
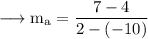
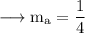
Since our line passes through A, the equation will be,
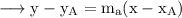
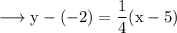
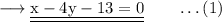

b. Finding equation of line passing through B and perpendicular to AC.

Since our line is perpendicular to AC, slope of the line is,
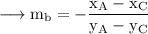
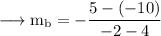
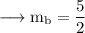
Since our line passes through B, the equation will be,
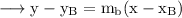
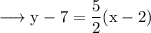
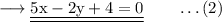

c. Finding point of intersection of the above two lines.

From (1),
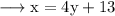
Putting this value of x in (2),
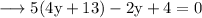
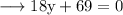
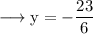
Then,
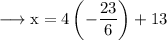
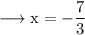
Hence the intersection point is