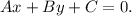Question

1. Find the equation of the straight line passing through the point (3, -2) and having the same gradient as the line 2y = 5x + 7.

*NOTE*please give an informative answer ​​

Answer 1

Explanation:

Our straight line has the same gradient as that of the line,

`2y=5x+7`

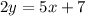
Dividing each term by 2,

`y=(5)/(2)\,x+(7)/(2)`

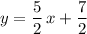
Now this equation is in the form
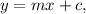`y=mx+c,` so the gradient of this line is 5/2.

So the gradient of our straight line is,

`m=(5)/(2)`

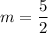
Given our straight line passes through the point,

`(x_1,\ y_1)=(3,\ -2)`

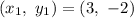
The equation of a straight line passing through a point
`(x_1,\ y_1)` and having gradient
`m` is given by,

`\longrightarrow\large\boxed{\quad y-y_1=m(x-x_1)\quad}`

This form of equation of a straight line is called point - slope form.

By this point - slope form, the equation of our straight line will be given by,

`\longrightarrow y-(-2)=(5)/(2)\,(x-3)`

`\longrightarrow y+2=(5)/(2)\,(x-3)`

`\longrightarrow2(y+2)=5(x-3)`

`\longrightarrow2y+4=5x-15`

`\longrightarrow\underline{\underline{5x-2y-19=0}}`

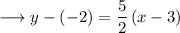
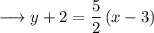
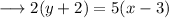
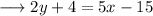
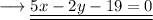
This is the equation of our straight line, written in the form
`Ax+By+C=0.`