Explanation:
We're asked to find the simplified form of,
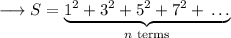
The n'th term of the sequence
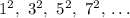 is
is
 So,
So,
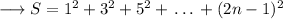
We know the following sum,
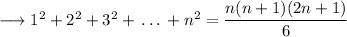
This is expression for the sum of squares of first 'n' natural numbers. In case of '2n' natural numbers,
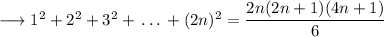
We separate odd squares and even squares in the LHS.
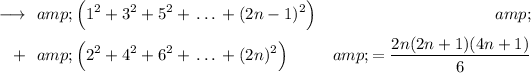
We can take 4 common from the sum of even squares.
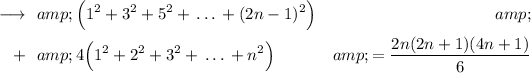
Now the sums in LHS are, as written above,
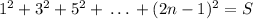
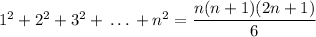
So,
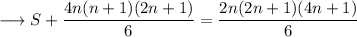
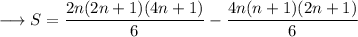
![\longrightarrow S=(2n+1)/(6)\Big[2n(4n+1)-4n(n+1)\Big]](https://img.qammunity.org/2023/formulas/mathematics/high-school/rkmtoor6qax5tqj4v7ih6p3vzi1u5ccfw0.png)
![\longrightarrow S=(2n+1)/(6)\Big[4n^2-2n\Big]](https://img.qammunity.org/2023/formulas/mathematics/high-school/qruekj70z18sfm41wp9fd5r202sqejws7c.png)
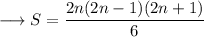
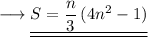
This is the expression for the sum of squares of first 'n' odd natural numbers.