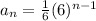Answer:
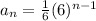
Explanation:
⭐What is the formula of a geometric sequence/progression?
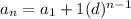
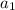 is the first term of the geometric sequence
is the first term of the geometric sequence
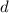 is the common ratio (the number each consecutive term gets multiplied by) of the geometric sequence
is the common ratio (the number each consecutive term gets multiplied by) of the geometric sequence
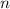 is the number term you want to find
is the number term you want to find
We are given the geometric sequence.
Thus, we need to find the first term and the common ratio, and substitute those values into the geometric sequence formula.
The first term is
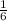
⭐How do we find the common ratio?
- divide one term by another term
- make sure both terms are consecutive of each other
I am choosing term 1 and term 2, but you can choose any other 2 terms that are consecutive.
term 1 =
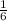
term 2 =

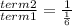
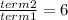
∴ The common ratio of this sequence is 6.
Now, substitute these values (common ratio & first term) into the geometric sequence equation.