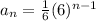Question

Which formula can be used to find the nth term of the geometric sequence 1/6,1,6,36?

Answer 1

`a_n = (1)/(6)(6)^(n-1)`

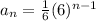
Explanation:

⭐What is the formula of a geometric sequence/progression?

• 
  `a_n = a_1+1(d)^(n-1)`
• 
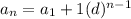
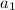  `a_1` is the first term of the geometric sequence
• 
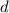  `d` is the common ratio (the number each consecutive term gets multiplied by) of the geometric sequence
• 
  `n` is the number term you want to find

We are given the geometric sequence.

Thus, we need to find the first term and the common ratio, and substitute those values into the geometric sequence formula.

The first term is
`(1)/(6)`

⭐How do we find the common ratio?

• divide one term by another term
• make sure both terms are consecutive of each other

I am choosing term 1 and term 2, but you can choose any other 2 terms that are consecutive.

term 1 =
`(1)/(6)`

term 2 =
`1`

`(term2)/(term1) = (1)/((1)/(6))`

`(term2)/(term1) = 6`

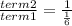
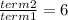
∴ The common ratio of this sequence is 6.

Now, substitute these values (common ratio & first term) into the geometric sequence equation.

`a_n = (1)/(6)(6)^(n-1)`