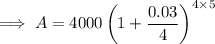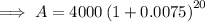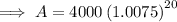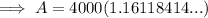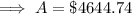Answer:


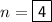
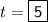
Explanation:

If you invest $4,000 then the principal amount is $4,000. As P represents the principal amount:

The interest is 3%. 3% = 3/100 = 0.03. Therefore:
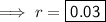
"n" represents the number of times interest is applied per year.
Therefore, if the interest is applied quarterly then:
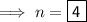
"t" represents the time in years. Therefore, if you plan to leave the money in the account for 5 years then:
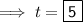
-----------------------------------------------------------------------------------------
To calculate the amount in the account after 5 years, substitute the values into the formula and solve for A: