Question

For questions 7 - 10, determine whether the angle of rotation is 90,180'or 270'. Each rotation is clockwise from the pre-image to the new image.

Answer 1

7) 180°

8) 90°

9) 270°

10) 180°

Explanation:

7)

The notation for rotating 180 degrees clockwise about the origin is (the degrees symbol was omitted):
`R_(-180, O) (x,y) - > (-x,-y)`

This means that when you rotate 180 degrees clockwise about the origin, the coordinates of the figure become their opposite.

C(2,-1) -> C'(-2,1)

N(4,-2) -> N'(-4,2)

W(3,-4) -> W'(-3,4)

Y(1,-3) -> (-1,3)

..............fun fact: rotating 180 degrees clockwise is the same as rotating 180 degrees counterclockwise

8)

The notation for rotating 90 degrees clockwise about the origin is (the degrees symbol was omitted):
`R_(-90, O) (x,y) - > (y,-x)`

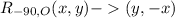
This means that when you rotate 90 degrees clockwise about the origin, the x and y coordinates flip, and the x coordinate becomes its opposite.

B(-4,-2) -> B'(-2,4)

E(-1,-5) -> E'(-5,1)

I(0,-1) -> I'(-1,0)

..............fun fact: rotating 90 degrees clockwise is the same as rotating 270 degrees counterclockwise

9) The notation for rotating 270 degrees clockwise about the origin is (the degrees symbol was omitted):
`R_(-270, O) (x,y) - > (-y,x)`

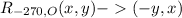
This means that when you rotate 270 degrees clockwise about the origin, the x and y coordinates flip, and the y coordinate becomes its opposite.

G(-4,2) -> G'(-2,-4)

Z(-1,5) -> Z'(-5,-1)

T(0,2) -> T'(-2,0)

..............fun fact: rotating 270 degrees clockwise is the same as rotating 90 degrees counterclockwise

10) The notation for rotating 180 degrees clockwise about the origin is (the degrees symbol was omitted):
`R_(180,O) (x,y) - > (-x,-y)`

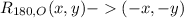
This means that when you rotation 180 degrees clockwise about the origin, the coordinates of the figure become their opposite.

B(-3,-5) -> B'(3,5)

G(-4,0) -> G'(4,0)

C(-5,-4) -> C'(5,4)

..............fun fact: rotation 180 degrees clockwise is the same as rotation 180 degrees counterclockwise

Answer 2

7/ 180 degree

8/ 90 degree

9/ 270 degree

10/ 180 degree

Explanation:

7/ Each square box is 90 degrees, and we see that the square rotated over 2 boxes, so it is 180 degrees clockwise.

8/ We see that the triangle rotated 90 degrees clockwise.

9/ We see that the triangles rotate over three boxes, which is 270 degrees clockwise.

10/ We see that the triangles rotate over 2 boxes, which is 180 degrees clockwise.