Answer:
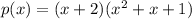


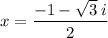
Explanation:
Given polynomial:
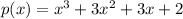
Rational Root Theorem
If P(x) is a polynomial with integer coefficients and if p/q is a root of P(x), then p is a factor of the constant term of P(x) and q is a factor of the leading coefficient of P(x).
Possible p-values
Factors of the constant term: ±1, ±2
Possible q-values
Factors of the leading coefficient: ±1
Therefore, all the possible values of p/q:
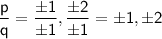
Substitute each possible rational root into the function:
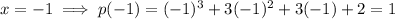
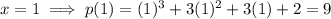
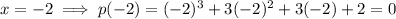
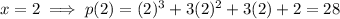
Therefore, x = -2 is a root of the polynomial since f(-2) = 0.
Divide the polynomial by the root using synthetic division:
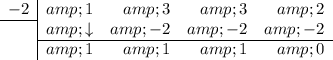
The bottom row (except the last number) gives the coefficients of the quotient. Therefore, the quotient is:
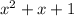
So the fully factored form of p(x) is:
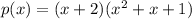

Therefore, the solutions to the quadratic factor are:
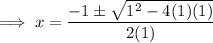
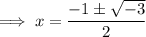


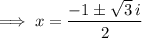
The 3 solutions of p(x) are: