The expanded form of
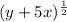 is
is
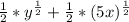 .
.
To expand the expression
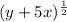 , we can use the binomial expansion formula. The binomial expansion of
, we can use the binomial expansion formula. The binomial expansion of
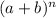 is given by:
is given by:
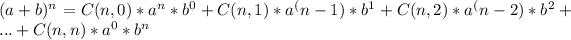
Where
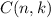 represents the binomial coefficient, which is given by
represents the binomial coefficient, which is given by
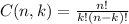 .
.
In our case,
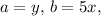 and
and
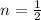 . We will expand it step by step:
. We will expand it step by step:
Step 1: Calculate
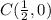
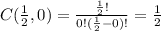
Step 2: Calculate
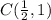
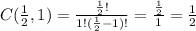
Now, we can use these coefficients to expand the expression:
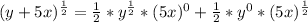
Step 3: Simplify the terms with
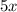 and
and
 :
:

Step 4: Further simplify the expression:
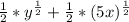
So, the answer is
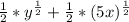 .
.