Question

Expanded form (y+5x)1/2

Answer 1

i couldn't fit the whole picture in there but hopefully this helps

Answer 2

The expanded form of
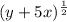`\((y+5x)^{(1)/(2)}\)` is
`\((1)/(2) * y^{(1)/(2)} + (1)/(2) * (5x)^{(1)/(2)}\)`.

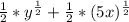To expand the expression
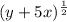`\((y+5x)^{(1)/(2)}\)`, we can use the binomial expansion formula. The binomial expansion of
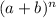`\((a+b)^n\)` is given by:

`\((a+b)^n = C(n,0) * a^n * b^0 + C(n,1) * a^(n-1) * b^1 + C(n,2) * a^(n-2) * b^2 + ... + C(n,n) * a^0 * b^n\)`

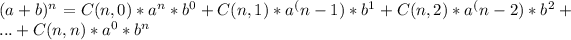
Where
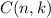`\(C(n, k)\)` represents the binomial coefficient, which is given by
`\(C(n, k) = (n!)/(k!(n-k)!)\)`.

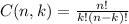In our case,
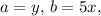`\(a = y\), \(b = 5x\),` and
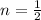`\(n = (1)/(2)\)`. We will expand it step by step:

Step 1: Calculate
`\(C((1)/(2), 0)\)`

`\(C((1)/(2), 0) = ((1)/(2)!)/(0!((1)/(2)-0)!) = (1)/(2)\)`

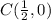
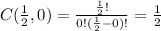
Step 2: Calculate
`\(C((1)/(2), 1)\)`

`\(C((1)/(2), 1) = ((1)/(2)!)/(1!((1)/(2)-1)!) = ((1)/(2))/(1) = (1)/(2)\)`

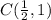
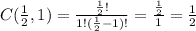
Now, we can use these coefficients to expand the expression:

`\((y+5x)^{(1)/(2)} = (1)/(2) * y^{(1)/(2)} * (5x)^0 + (1)/(2) * y^0 * (5x)^{(1)/(2)}\)`

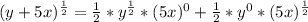
Step 3: Simplify the terms with
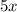`\(5x\)` and
`\(y^0\)`:

`\((1)/(2) * y^{(1)/(2)} * 1 + (1)/(2) * 1 * (5x)^{(1)/(2)}\)`

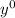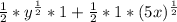
Step 4: Further simplify the expression:

`\((1)/(2) * y^{(1)/(2)} + (1)/(2) * (5x)^{(1)/(2)}\)`

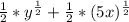
So, the answer is
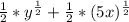`\((1)/(2) * y^{(1)/(2)} + (1)/(2) * (5x)^{(1)/(2)}\)`.