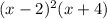Answer:
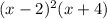
Explanation:
For
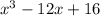 we can test out different values of x until the polynomial is zero, in this case 2 works so we can use long division or seperation of terms and factoring. But to show work, I will use seperation and factor.
we can test out different values of x until the polynomial is zero, in this case 2 works so we can use long division or seperation of terms and factoring. But to show work, I will use seperation and factor.
 =
=

=

Then we can factor the second-degree polynomial to get
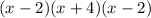 or
or