Answer:
Second central moment =
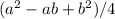
Third central moment =
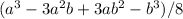
Explanation:
The second central moment (also known as the variance) of a variable that takes two distinct values a and b, each with equal frequency, is given by:
Second central moment = (a - mean)^2 * frequency(a) + (b - mean)^2 * frequency(b)
where mean is the mean value of the variable, frequency(a) is the frequency with which the value a occurs, and frequency(b) is the frequency with which the value b occurs.
Since the values a and b have equal frequency, the mean value of the variable is simply the average of a and b:
mean = (a + b) / 2
Substituting this expression for the mean into the formula for the second central moment, we get:
Second central moment = (a - ((a + b) / 2))^2 * frequency(a) + (b - ((a + b) / 2))^2 * frequency(b)
= (a^2 - ab + b^2) / 4
The third central moment (also known as the skewness) of a variable that takes two distinct values a and b, each with equal frequency, is given by:
Third central moment = (a - mean)^3 * frequency(a) + (b - mean)^3 * frequency(b)
Substituting the expression for the mean and the frequencies into this formula, we get:
Third central moment = (a - ((a + b) / 2))^3 * (1/2) + (b - ((a + b) / 2))^3 * (1/2)
= (a^3 - 3a^2b + 3ab^2 - b^3) / 8
I hope this helps! Let me know if you have any questions.