Question

A variable takes only two distinct values a and b, each with equal frequency. Find the second and

third central moments.

Answer 1

Second central moment =
`(a^2 - ab + b^2) / 4\\`

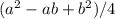
Third central moment =
`(a^3 - 3a^2b + 3ab^2 - b^3) / 8`

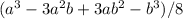
Explanation:

The second central moment (also known as the variance) of a variable that takes two distinct values a and b, each with equal frequency, is given by:

Second central moment = (a - mean)^2 * frequency(a) + (b - mean)^2 * frequency(b)

where mean is the mean value of the variable, frequency(a) is the frequency with which the value a occurs, and frequency(b) is the frequency with which the value b occurs.

Since the values a and b have equal frequency, the mean value of the variable is simply the average of a and b:

mean = (a + b) / 2

Substituting this expression for the mean into the formula for the second central moment, we get:

Second central moment = (a - ((a + b) / 2))^2 * frequency(a) + (b - ((a + b) / 2))^2 * frequency(b)

= (a^2 - ab + b^2) / 4

The third central moment (also known as the skewness) of a variable that takes two distinct values a and b, each with equal frequency, is given by:

Third central moment = (a - mean)^3 * frequency(a) + (b - mean)^3 * frequency(b)

Substituting the expression for the mean and the frequencies into this formula, we get:

Third central moment = (a - ((a + b) / 2))^3 * (1/2) + (b - ((a + b) / 2))^3 * (1/2)

= (a^3 - 3a^2b + 3ab^2 - b^3) / 8

I hope this helps! Let me know if you have any questions.