Question

1. Find the equation of the straight line that passes through the points (0, -1) and (-1,0).

2. For this problem, please use the point-gradient form of the equation that passes through
the points (2, -4) and has gradient/slope 3.
3. Find the equation of the straight line that is parallel to the line y = x-2 and goes through
the point (0,1). Use Desmos Graphing Calculator to check your answer.

Answer 1

1) y = -x -1

2) y + 4 = 3( x -2)

3) y = x + 1

Explanation:

1)

The slope is the change in y over the change in x. The y values from the points given is 0 and -1. The x values from the points given is -1 and o

Slope:
`(o - -1)/(-1 - o)` =
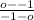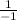`(1)/(-1)` = -1

y -intercept

y = mx + b Use the point (0,-1) and the slope to solve for b

y = -1

m = -1

x = 0

y = mx + b

-1 = -1(0) + b

-1 = 0 + b

-1 = b This is the y intercept.

y = mx + b

y = =x -1

2)

point-gradient form is

y -y = m (x-x)

y - -4 = 3 (x -2)

y + 4 = 3( x - 2)

3)

Parallel lines have the same slope.

slope is 1. Use this and the point (0,1) to solve for b

y = mx + b

1 = 1(0) + b

1 = 0 + b

1 = b

y = x + 1