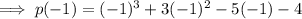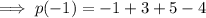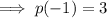Answer:
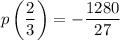
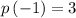
Explanation:
Remainder Theorem
When we divide a polynomial p(x) by (x − a) the remainder is p(a).
Given:
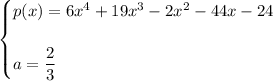
To find p(a), set up the synthetic division problem with the coefficients of the polynomial p(x) as the dividend and "a" as the divisor.
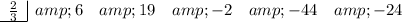
Bring the leading coefficient straight down:
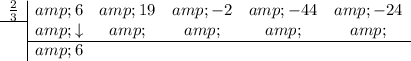
Multiply the number you brought down with the number in the division box and put the result in the next column (under the 19):
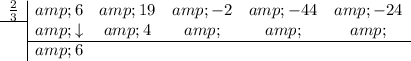
Add the two numbers together and put the result in the bottom row:
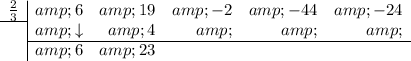
Repeat:
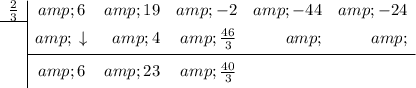
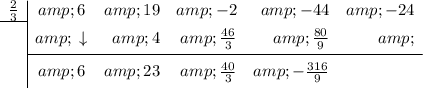
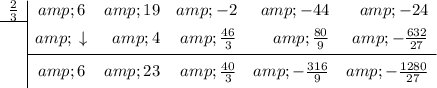
The last number (remainder) is
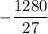
Therefore, according to the remainder theorem:
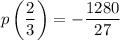
Check by substituting a = 2/3 into p(x):
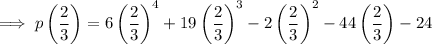
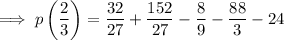
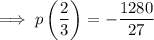
-------------------------------------------------------------------------------------------------
Given:
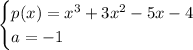
To find p(a), set up the synthetic division problem with the coefficients of the polynomial p(x) as the dividend and "a" as the divisor.
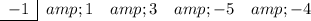
Bring the leading coefficient straight down:

Multiply the number you brought down with the number in the division box and put the result in the next column (under the 3):
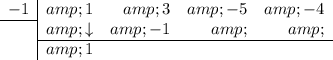
Add the two numbers together and put the result in the bottom row:
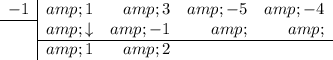
Repeat:
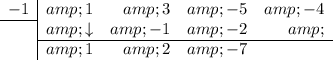
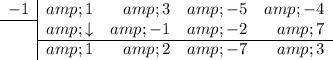
The last number (remainder) is 3.
Therefore, according to the remainder theorem:
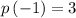
Check by substituting a = -1 into p(x):