Question

Aimee packs ice cream into an ice cream cone. She then puts a perfect hemisphere of ice cream on top of the cone that has a volume of 4 in.3 The diameter of the ice cream cone is equal to its height. What is the total volume of ice cream in and on top of the cone? Use the relationship between the formulas for the volumes of cones and spheres to help solve this problem. Show your work and explain your reasoning.

(4 points)

Answer 1

8 in³

Explanation:

`\boxed{\begin{minipage}{4 cm}\underline{Volume of a sphere}\\\\$V=(4)/(3) \pi r^3$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \end{minipage}}`

Since "hemi" is a prefix meaning one half, the volume of a hemisphere is one half the volume of a sphere:

`\implies V_(\sf hemisphere)=((4)/(3)\pi r^3)/(2)`

`\implies V_(\sf hemisphere)=(2)/(3)\pi r^3`

`\boxed{\begin{minipage}{4 cm}\underline{Volume of a cone}\\\\$V=(1)/(3) \pi r^2 h$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \phantom{ww}$\bullet$ $h$ is the height.\\\end{minipage}}`

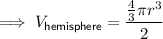
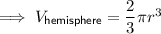
Given the diameter of the ice cream cone is equal to its height:

• diameter = h = 2r

Substitute h = 2r into the equation for the volume of the cone:

`\implies V_(\sf cone)=(1)/(3) \pi r^2 \cdot 2r`

`\implies V_(\sf cone)=(2)/(3) \pi r^3`

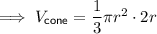
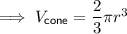
Therefore, we can see that the formula for the volume of ice cream in the cone is the same as the formula for the volume of the hemisphere of ice cream.

This means that the volume of the cone of ice cream is equal to the volume of the hemisphere of ice cream.

Given the volume of the hemisphere is 4 in³, the total volume of the ice cream is 8 in³.