Question

Given the drawing as shown below and that p parallel q, which of the following cannot be supported?​

Answer 1

Answer: It's B

Explanation:

It shows that Angle B is congruent to angle g but it actually isnt

Answer 2

B. ∠b ≅ ∠g

Explanation:

Supplementary angles

Two angles whose measures sum to 180°.

Linear Pair

Two adjacent angles that sum to 180° (two angles which when combined together form a straight line).

Same-side Interior Angles Theorem

When two parallel lines are intersected by a transversal, the angles that are interior to the parallel lines and on the same side of the transversal line are supplementary (sum to 180°).

Vertical Angles Theorem

When two straight lines intersect, the opposite vertical angles are congruent.

------------------------------------------------------------------------------------------

Statement A

∠f and ∠h are vertical angles. Therefore, according to the Vertical Angle Theorem, ∠f ≅ ∠h.

Statement C

As ∠d and ∠h are the interior angles on the same side of the transversal
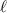`\ell`, according to the Same-side Interior Angles Theorem, ∠d and ∠h are supplementary.

Statement D

∠a and ∠b are a linear pair, therefore ∠a and ∠b are supplementary.

Therefore, Statement B cannot be supported by the evidence shown.