Question

PLEASE HELP!

P(x)=x^3 - 4x^2 - 1
Where P is in hundreds of dollars and x is the number of years elapsed since the start up year

Answer 1

Yes, the company will break even at some point in time

Explanation:

I am not sure what methodology your teacher has been using. I am going to provide a simple methodology

• The polynomial function for profit is
  
  `p(x) = x^3 - 4x^2 - 1`

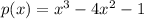
• If
  `p(x)`has at least one zero then that means it will intersect the x-axis and the company will break even(Revenue = Costs)
  

• The zeros of
  `p(x)` are the values of x where
  `p(x) = 0`
  

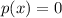
• So if we can find out if
  `p(x)` ever crosses the x-axis then that would indicate that the company will break-even at some value of
  `x` years. If not, the company will never break even.
  

• There is a rule to determine how many zeros a polynomial will have or in other words how many times it crosses the x-axis. This is known as Descartes' Rule of Signs.
  

• Briefly the rule states that the number of zeros can be determined by the number of sign changes in the polynomial for consecutive terms

• p(x) can be re-written as:
  +x³ - 4x² - 1

• If we look at the signs we see + - -

• Therefore there is one sign change from + to -

• This means p(x) will have one zero

Therefore the company will break-even at some point

Other Notes

• You can also solve for the roots of the polynomial and see how many real roots are there. In this case there is one real root at
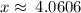  `x\approx \:4.0606`. But that is a lot of work

• Another way to approach this problem is to simply graph the function and see if it crosses the x axis. I have provided the graph of this function and you can see that it does cross the x-axis at
  `x = 4.06`

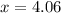
I hope that helps you