Answer:
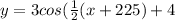 phase shift in degrees
phase shift in degrees
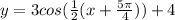 phase shift in pi radians
phase shift in pi radians
Explanation:
Here is the equation for the graph of the cosine function.
y = A sin(B(x + C)) + D
A = amplitude
period is 2π/B
C = phase shift
D = vertical shift
Lets convert 1800° to Pi radians.

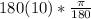
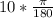
 radians
radians
A = 3
B=2π/ 10π simplifies to

C = phase shift
D = 4
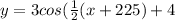 phase shift in degrees
phase shift in degrees
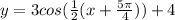 phase shift in pi radians
phase shift in pi radians